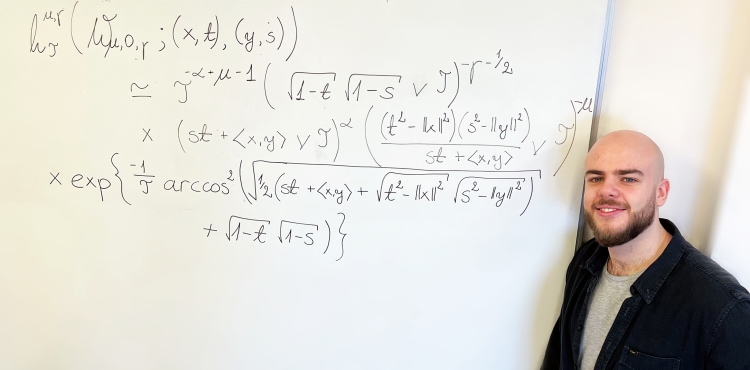
Dawid Hanrahan zajął drugie miejsce w konkursie im. Józefa Marcinkiewicza na najlepszą pracę z zakresu matematyki. Nagrodę przyznało mu Polskie Towarzystwo Matematyczne, które wyróżniło też pracę naszego doktoranta Mateusza Śliwińskiego.

Jury doceniło pracę dyplomową absolwenta Wydziału Matematyki pt. ,,Ostre oszacowanie jądra ciepła Jacobiego na stożku" napisaną pod opieką dr. Dariusza Kosza.

Dawid Hanrahan zmierzył się w niej z ambitnym problemem, dotyczącym współcześnie rozwijającej się gałęzi matematyki. Uzyskał on obustronne oszacowanie dla jądra ciepła Jacobiego na wielowymiarowym stożku dla małych wartości parametru czasu. Połączył własne obserwacje na temat równania ciepła oraz geometrii stożka ze znanymi metodami wykorzystywanymi w kontekście pokrewnych zagadnień.

Warto podkreślić typ otrzymanego przez absolwenta PWr oszacowania. Termin „ostry” wskazuje na znalezienie funkcji ograniczających z dołu i z góry, posiadających tę samą stałą w eksponencie. Jest to istotnie silniejszy wynik od spotykanych znacznie częściej w literaturze oszacowań „jakościowo ostrych”, które pozwalają na użycie różnych stałych w eksponentach dwóch wyrażeń szacujących. Tak precyzyjny opis zachowania jądra ciepła udało się otrzymać jak dotąd jedynie w kilku szczególnych sytuacjach.

Dlaczego to takie interesujące?

Dawid Haranhan od początku swojej nauki na PWr mocno interesował się analizą matematyczną. – Udałem się do jednego z prowadzących z zapytaniem o dodatkowe materiały, książki czy zadania. Polecił mi podręcznik związany z jedną z najnowocześniejszych gałęzi klasycznej analizy, tzw. analizą harmoniczną. Ta dziedzina tak mi się spodobała, że postanowiłem się nią zająć – wyjaśnia laureat.

Swoją pracę licencjacką, związana z oszacowaniami jąder ciepła na prostej, napisał pod okiem prof. Jacka Małeckiego, we współpracy z prof. Adamem Nowakiem z Polskiej Akademii Nauk Gdy jednak w 2019 roku profesor Xu opublikował pracę, w której opisał układ ortogonalny wielomianów na stożku, a obiekt ten jest niezbędny do zapisania jądra ciepła, w naturalny sposób powstał kolejny problem do rozwiązania. Nowe jądro wymagało nowych oszacowań. – Miałem już trochę doświadczenia w tym temacie i znałem narzędzia, które w takich problemach są wykorzystywane, stąd decyzja o napisaniu pracy o tym właśnie aspekcie – dodaje laureat.

***

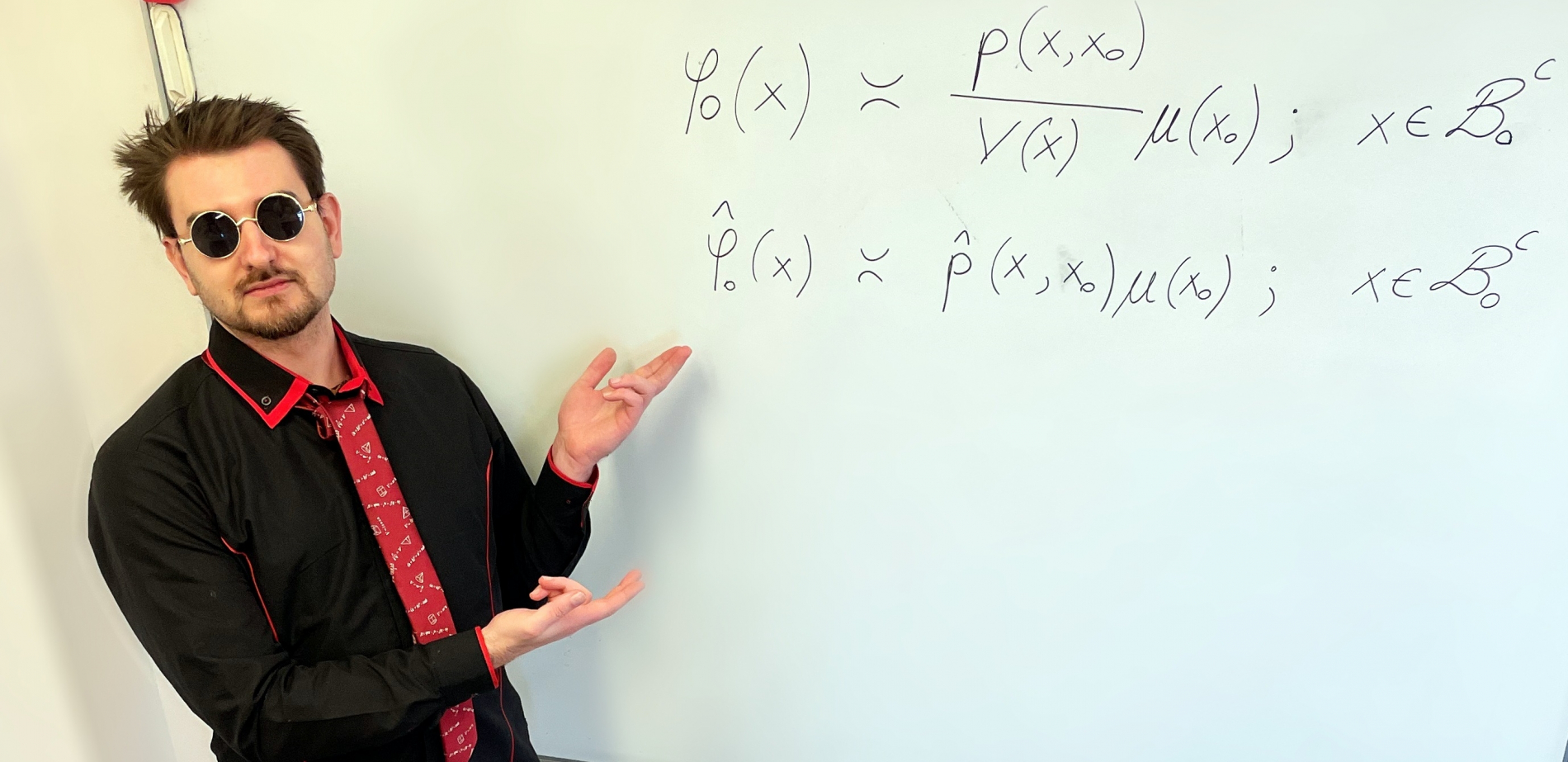
W konkursie wyróżniono również pracę doktoranta Wydziału Matematyki Mateusza Śliwińskiego zatytułowaną ,,Oszacowania funkcji własnych dla oscylatorów kwantowych na grafach".

– Jej temat zaproponował mój promotor dr hab. inż. Kamil Kaleta i była to de facto kontynuacja tego, co opisałem w pracy licencjackiej, tylko w ogólniejszym zakresie i przy nieco innych założeniach – wyjaśnia Mateusz Śliwiński.

Autor wyróżnionej pracy łączy w niej procesy stochastyczne (losowo zmieniające się w czasie) oraz analizę funkcjonalną, aby otrzymać wyniki, które mają zastosowanie np. w mechanice kwantowej. Tytułowe oscylatory kwantowe są bowiem ważnym obiektem badań tej dziedziny fizyki.

– Wiemy, że funkcja własna tzw. stanu podstawowego oscylatora z drgającą cząstką pozwala przewidywać, gdzie owa cząstka może się znajdować, gdy układ zmienia się w czasie – mówi Mateusz Śliwiński. – Moje wyniki pozwalają oszacować funkcje własne takich oscylatorów, nawet jeśli ich dokładna postać nie jest znana. Urokiem tego tematu jest to, że mimo dość wysokiego „progu wejścia”, dowody i rozumowania, z których wyprowadza się te wnioski, są dosyć proste – dodaje doktorant.

Więcej informacji oraz pełna lista laureatów na stronie PTM.